本文将介绍如何在CAD软件中绘制三角形的内切圆。内切圆是指一个可以与三角形的三个边都相切的圆。在几何学中，这是一种基本构造，经常用于解决各种几何问题和设计应用。在CAD中进行这类绘图需要结合精确的数学计算和工具的熟练运用。通过学习这一技法，你将掌握更复杂图形的绘制技巧，并且能够提升你的计算机辅助设计能力。

首先，我们需要明确一些基础概念。三角形的**内切圆**位于三角形的内部，其触点分别位于三角形的各边上。这些触点也称为切点。内切圆的圆心（即三角形的内心）是从三角形的每个内角作内角平分线，三条平分线交于一点，此交点即为内切圆的圆心。在CAD中绘制三角形的内切圆，你需要按照以下步骤进行：1. **画出三角形**：使用CAD工具中的“多段线”指令（通常是命令栏中的`PLINE`），根据所需的三角形顶点坐标依次连接，以形成一个封闭的三角形。确保输入的坐标值准确，因为接下来的计算基于这些点。2. **找出三角形的内心**：如前所述，内心是由三角形的三个内角平分线相交得到的点。在CAD中，可以使用“角平分线”命令，或者手动计算并绘制。这需要测量每个角，并在每个角的两条边间找到平分线的位置。3. **手动角平分线的绘制**：选择一个角，使用“角度”功能来确定平分线方向。一旦确定这个方向，通过直线工具`LINE`延长至两条边的交点。对另外两个角重复此操作。4. **确定内切圆半径**：内切圆的半径可通过公式求得：设三角形的三边长分别为a、b、c，三角形的半周长为s，那么内切圆的半径r可用公式：r = A/s，其中A为三角形的面积，s为半周长，s = (a+b+c)/2。5. **计算三角形面积**：利用海伦公式：A = √[s(s-a)(s-b)(s-c)]。在CAD中不需要手工计算，你可以加入插件或编程扩展以自动化这一过程。6. **绘制内切圆**：使用“圆”工具，根据已经确定的内心作为圆心画出半径为r的圆。这涉及到合适的比例调整，以便在视图中清晰可见。7. **检查和调整**：一旦初始绘制完成，用“距离”命令检查圆是否与三边精确相切。如有误差，再次检验前面的步骤，确认每个计算和绘制均无误。8. **标注补充**：最后，可以使用“标注”功能添加额外的信息，例如半径尺寸、内心坐标等。这对于日后的修改或查看是十分便利的。通过以上步骤，在CAD环境下创建一个精确的**内切圆**不仅锻炼了空间想象能力，更提高了对软件功能的综合应用水平。掌握这些技能后，不仅可以处理简单的几何问题，还能为复杂的设计项目提供数学上的支持和视觉上的表现。进一步可以探索CAD软件中的高级功能，如脚本编写和宏命令，以使这些过程更加自动化和高效。这不仅可以节省时间，也大大减少人为错误，为工程设计及建筑项目中的实际应用打下坚实的基础。总之，CAD软件的灵活性和强大功能为实现这样的几何绘图提供了无限可能，借助这些技术，你可以轻松地模拟和设计出具有挑战性的图形和结构。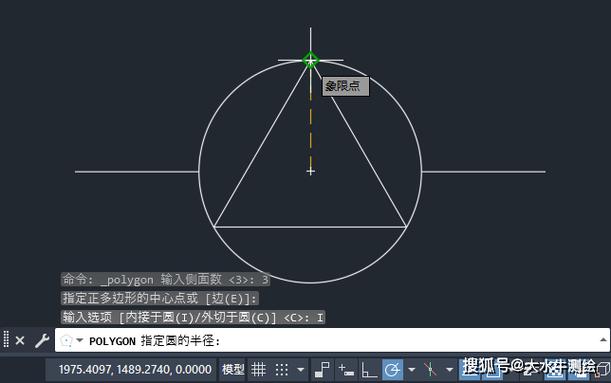

BIM技术是未来的趋势，学习、了解掌握更多BIM前言技术是大势所趋，欢迎更多BIMer加入BIM中文网大家庭（http://www.wanbim.com），一起共同探讨学习BIM技术，了解BIM应用！