本文概述：极坐标是描述几何图形的一种重要方式，尤其是在一些特殊的应用场景中，如物理学和工程学等领域。通过掌握极坐标追踪画线的练习题，可以帮助学习者深入理解极坐标系统的特性及其实际应用。

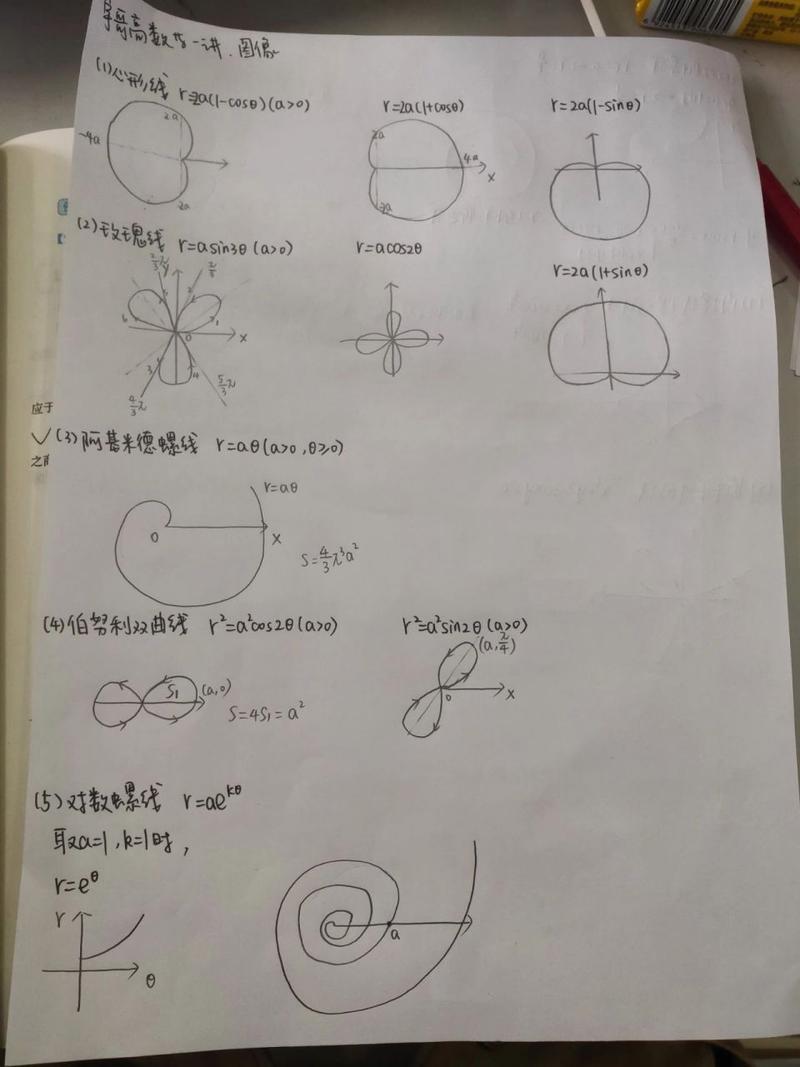
在处理几何问题时，**极坐标系统**可以为我们提供一种不同于直角坐标系的视角。在传统的平面直角坐标系中，我们用横纵坐标来定义点的位置，但在极坐标系中，点的定位通过两项量度：**径向距离**（通常记作r）和**角度θ**。这种表示方法非常适合描述那些具有**圆对称性**的现象。

第一个重点

是“**极坐标的基本概念**”。在极坐标系统中，原点称为极点，而与正方向x轴重合的射线称为极轴。任何一点P都可以用一个有序对(r, θ)来表述，其中r表示从极点到点P的径向距离，θ表示从极轴到经过点P的直线的夹角。正值的r表示点位于极点外，负值表示在极点反向延长线上。θ则通常以弧度或度数为单位测量，这一角度可以使得点在整个平面内旋转两周或者更多，这是由于极坐标的周期性特点。
了解了这些基础后，让我们看看**极坐标追踪画线的步骤**。当我们谈论极坐标追踪画线时，实际上是在解决如何利用极坐标方程生成各种几何图形的问题。接下来，我们通过几个实例说明相关的步骤和技巧。

第二个重点

是“**画简单的极坐标线**”。假设给定一个函数r=f(θ)，其描述了一条曲线。第一题可能涉及一个常见的极坐标图——圆。例如，如果f(θ) = a（a为常数），那么这个方程实际表示的是一个以极点为圆心，半径为a的圆。这是因为对于所有θ而言，r都是恒定的，从而点始终距离极点相同。

第三个重点

是“**绘制螺旋线**”。假如你遇到的方程为r = aθ（其中a为常数），这就是典型的阿基米德螺旋线。这样的方程意味着随着θ的增加，r也根据比例因素a不断增大。这种方程广泛用于描述无缝卷绕的金属管、记录播放设备中的磁性音轨，并且在计算机科学中用于某些递归算法。

第四个重点

是“**考虑对称性**”。极坐标图形往往具有对称性，比如玫瑰花图。这个图由公式r=a*sin(kθ)或r=a*cos(kθ)描述，其形态受k值控制。当k是整数时，图形显示出2k个花瓣（如果k为偶数），否则为k个花瓣。这样的图形被用于艺术设计和信号分析中。

第五个重点

是“**精确绘制曲线**”。为了准确描绘复杂的极坐标曲线，最好根据θ的范围和变化率逐步计算相应的r值，然后将每组(r, θ)转换为直角坐标(x, y)。通过一系列**练习题**，学习者不仅可以熟悉基本的极坐标操作，还能更好地理解这些数学工具在实际问题中的应用。这是一个理论与实践结合的过程，掌握这一技能将为多学科的研究和工程项目提供极大的便利。因此，逐个攻克这些难题，不仅能够提升你的数学能力，也能够为你打下坚实的技术基础。

BIM技术是未来的趋势，学习、了解掌握更多BIM前言技术是大势所趋，欢迎更多BIMer加入BIM中文网大家庭（http://www.wanbim.com），一起共同探讨学习BIM技术，了解BIM应用！